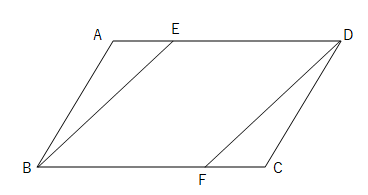
中点連結定理を使った平行四辺形であることの証明 教遊者
と書く事もできるので平行四辺形の法則とも言われる。 内積空間における中線定理 中線定理は内積を有するベクトル空間（内積空間、計量ベクトル空間）の一般的性質としてとらえることができる。内積空間v に対し、内積によって定義されたノルム数学の問題を解くときに、定義や定理という言葉を目にすることがあります。 今回は、 定義 と 定理 の違いについて説明します。 定義 定義とは、 言葉の意味を明確に述べたもの です。 例えば、平行四辺形という図形を考えてみます。
平行四辺形の定義 定理
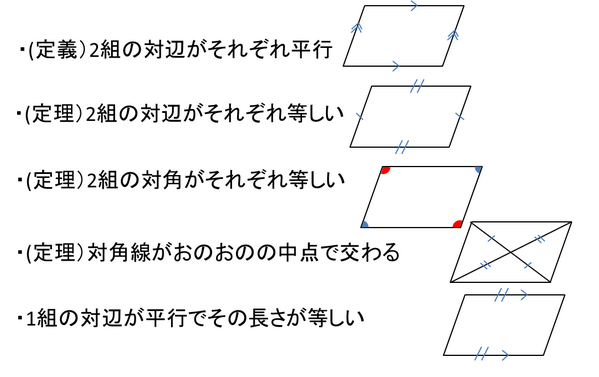
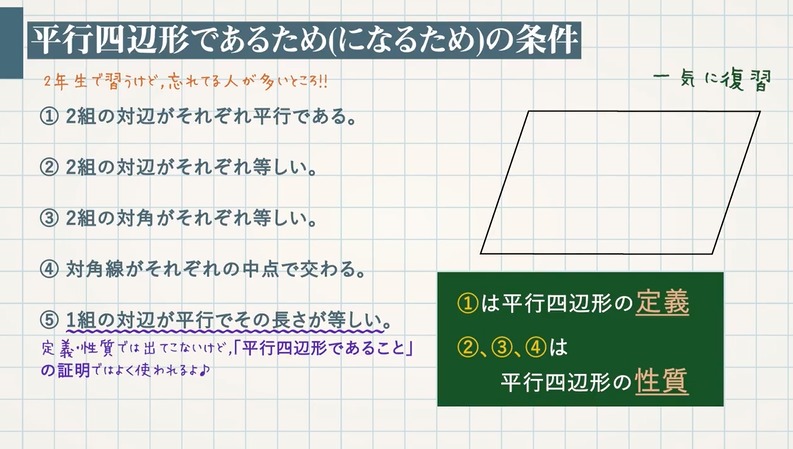
平行四辺形の定義 定理-定義 2組の向かい合う辺が平行な四角形を平行四辺形という 定理 平行四辺形の2組の向かい合う辺の長さはそれぞれ等しい 定理 平行四辺形の2組の向かい合う角の大きさはそれぞれ等しい 定理 平行四辺形の対角線はそれぞれ中点で交わる 円に内接する四角形の内角は、その対角の外角と等しい平行四辺形の定義・定理（性質）と証明問題：中学数学の図形 リョースケ大学 「定義」と「定理」の違いとは？｜三郷・吉川の学習塾｜小島進学セミナー;
平行四辺形に関する定理 雑学のソムリエ
対角線の長さが等しく、それぞれの中点で交わるとき、長方形になる。（証明） ひし形になる条件 対角線がそれぞれの中点で垂直に交わるとき、ひし形になる。（証明） 問題 1 平行四辺形abcdが、次の条件をもつと、それぞれ、どんな四角形になりますか。 中2数学「平行四辺形の性質の定期テスト過去問分析問題」です。 平行四辺形の定義 定義2組の向かいあう辺が、それぞれ平行な四角形 平行四辺形の性質（定理） 平行四辺形の2組の向かいあう辺は、それぞれ等しい。 平行四辺形の2組の向かいあ平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。
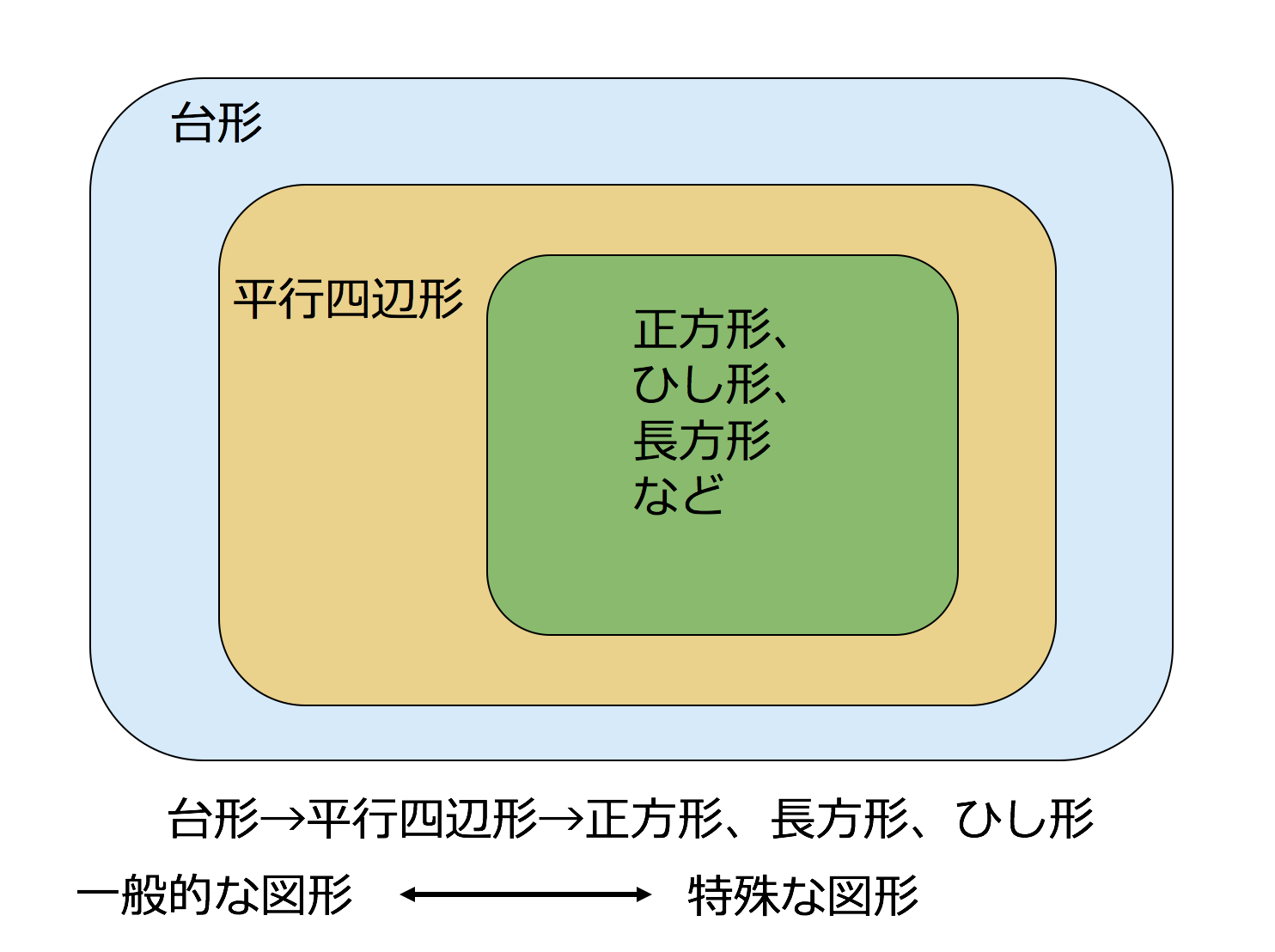
証明平行四辺形定義と定理 64 491 0 関連ノート 意味定義と定理 合同の証明二等辺三角形の利用 合同の証明二等辺三角形であることの証明 合同の証明平行であることの証明 合同の証明平行と合同 このノートについて マジック配信中 中学全学年 証明の書き方の説明です。 定義と定理の扱い方は、関連ノートを見てください 三角形と四角形 数学平行四辺形の定義は 「2組の対辺が、それぞれ平行である四角形」 平行四辺形の定理 1 平行四辺形の2組の対辺は、 それぞれ等しい。 2 平行四辺形の2組の対角は、 それぞれ等しい。 3 平行四辺形の対角線は、 それぞれの中点で交わる。 1 2組の対辺が平行四辺形： 対角線が 互いの中点で交わる 長方形： 対角線が 互いの中点で交わる ＆ 長さが等しい ひし形： 対角線が 互いの中点で交わる ＆ 直交する 正方形： 対角線が 互いの中点で交わる ＆ 直交する ＆ 長さが等しい 台形： 特になし 平行四辺形は2本の対角線がそれぞれの真ん中で交わります。 長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、
平行四辺形の定義 定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
3 |  3 |  3 |
3 |  3 |  3 |
3 |  3 | 3 |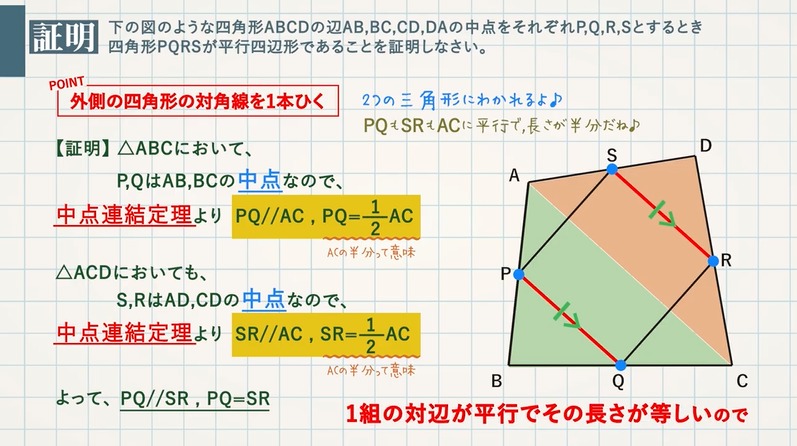
 3 |  3 |  3 |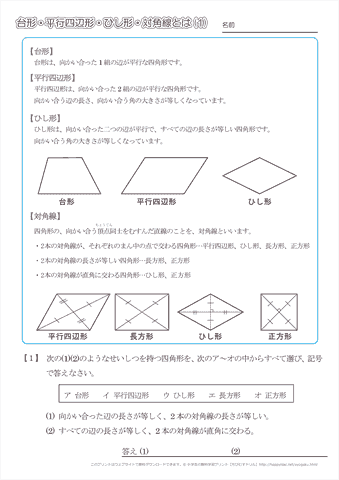
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 | 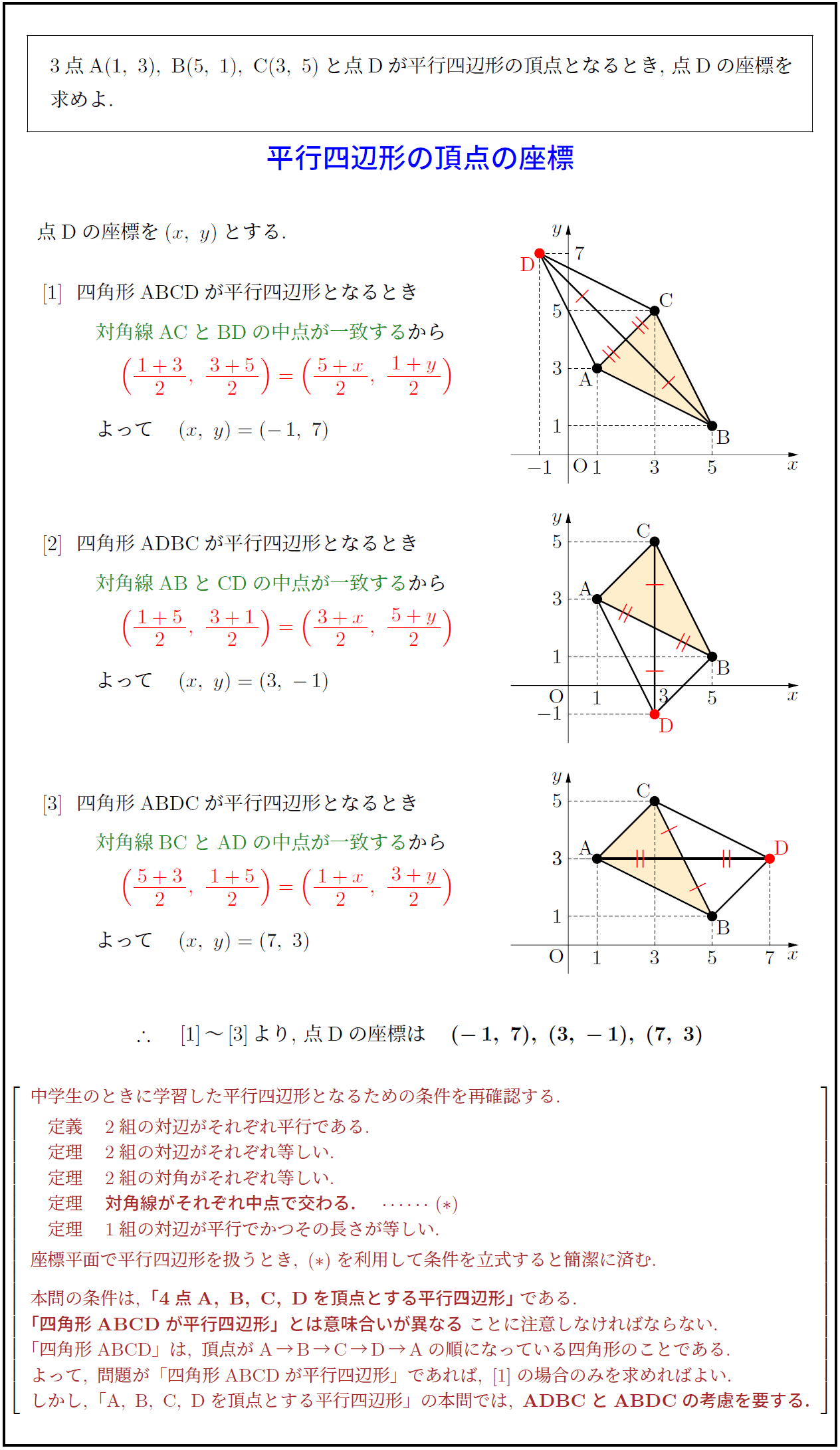3 |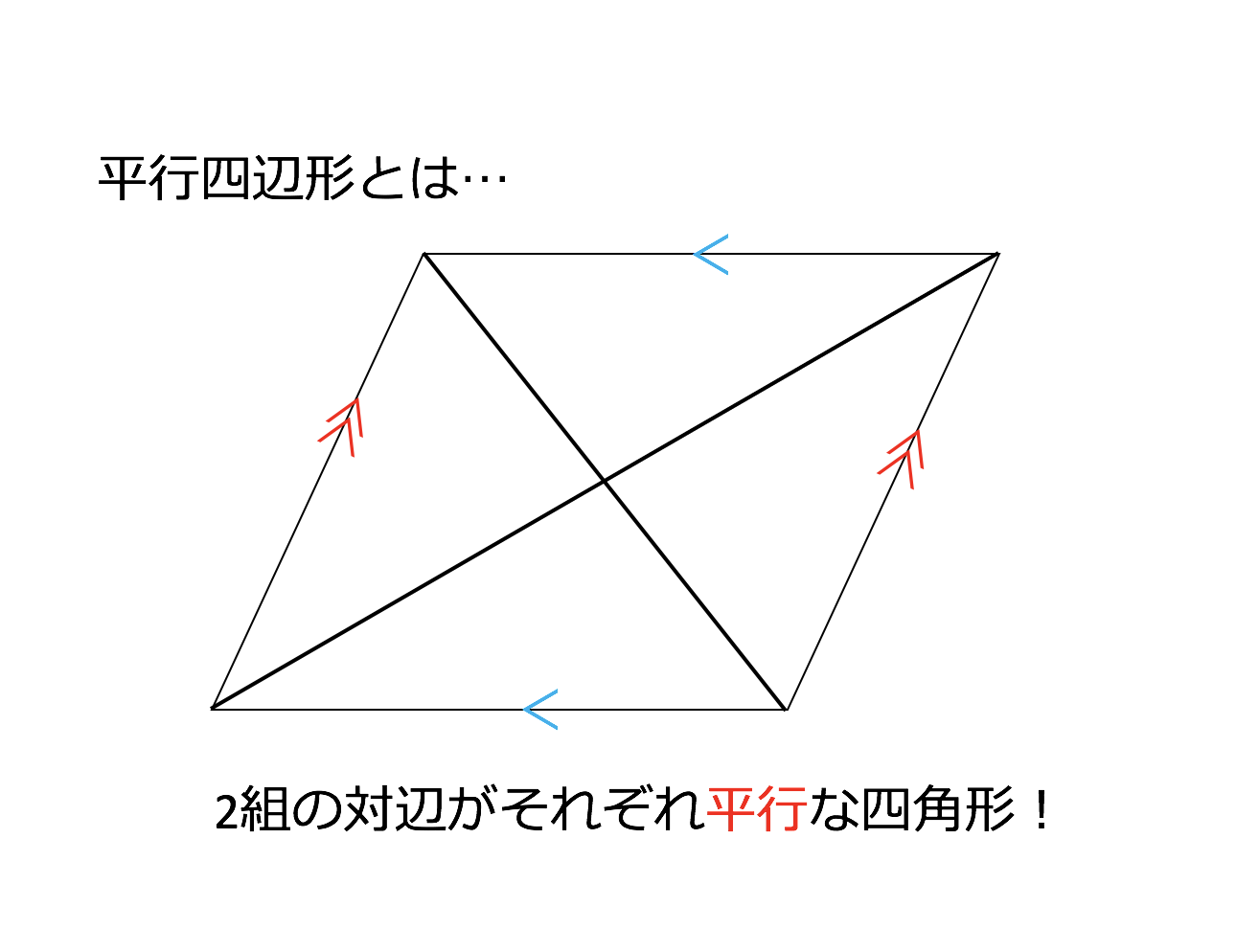
 3 |  3 |  3 |
 3 |  3 |  3 |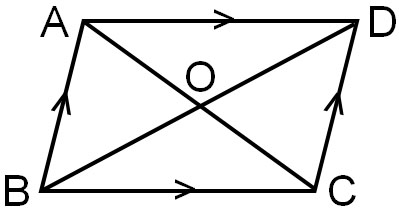
 3 | 3 | 3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |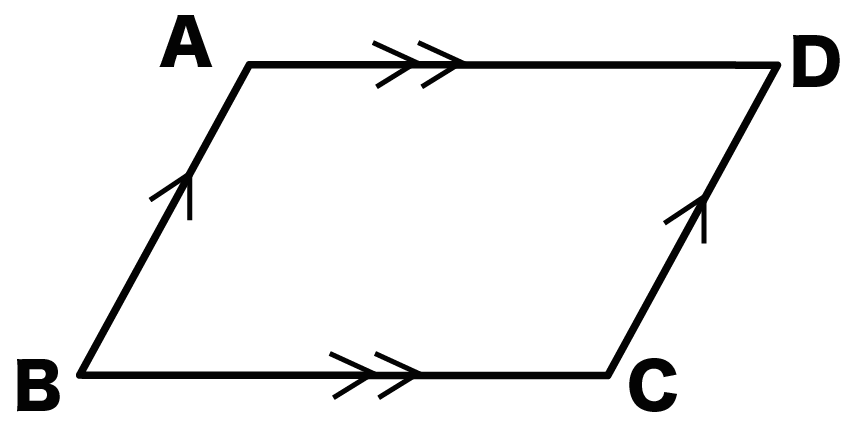
 3 |  3 |  3 |
 3 |  3 |  3 |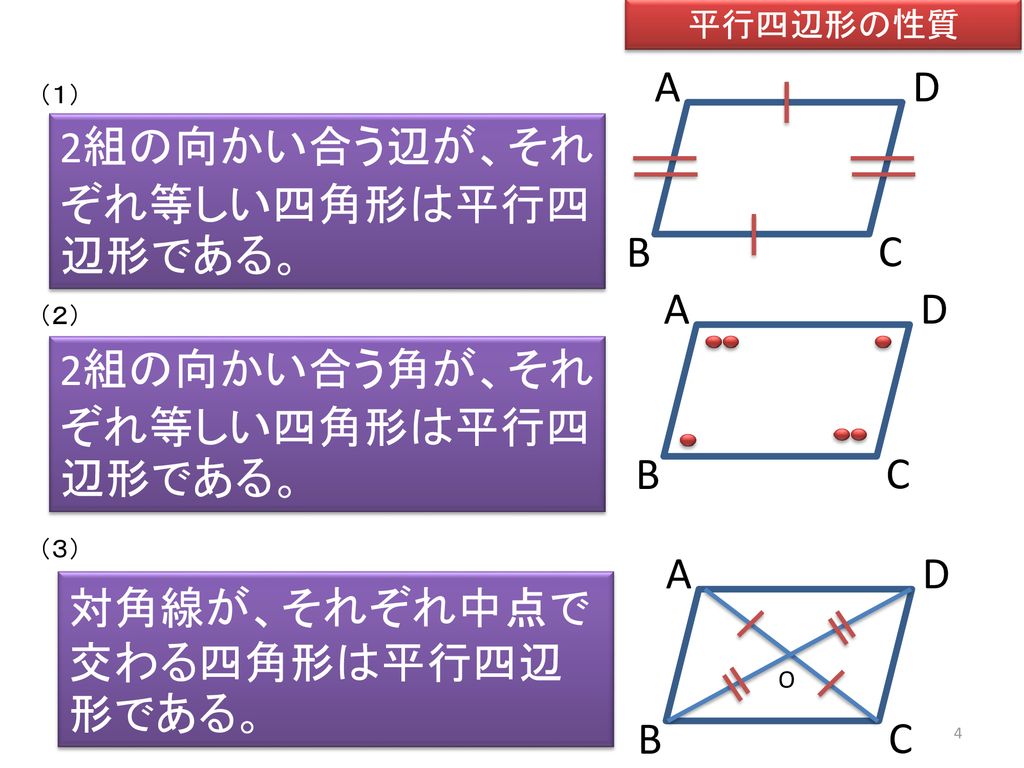
 3 | 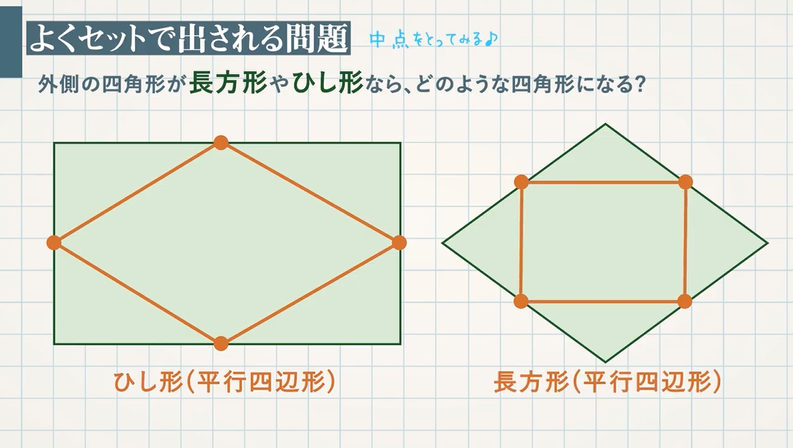3 |  3 |
 3 | 3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |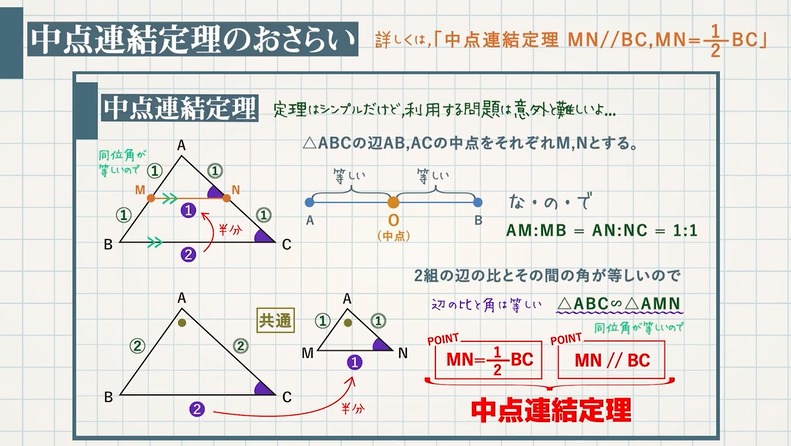
 3 |  3 |  3 |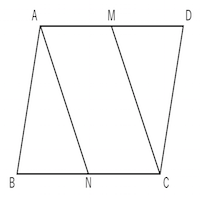
 3 | 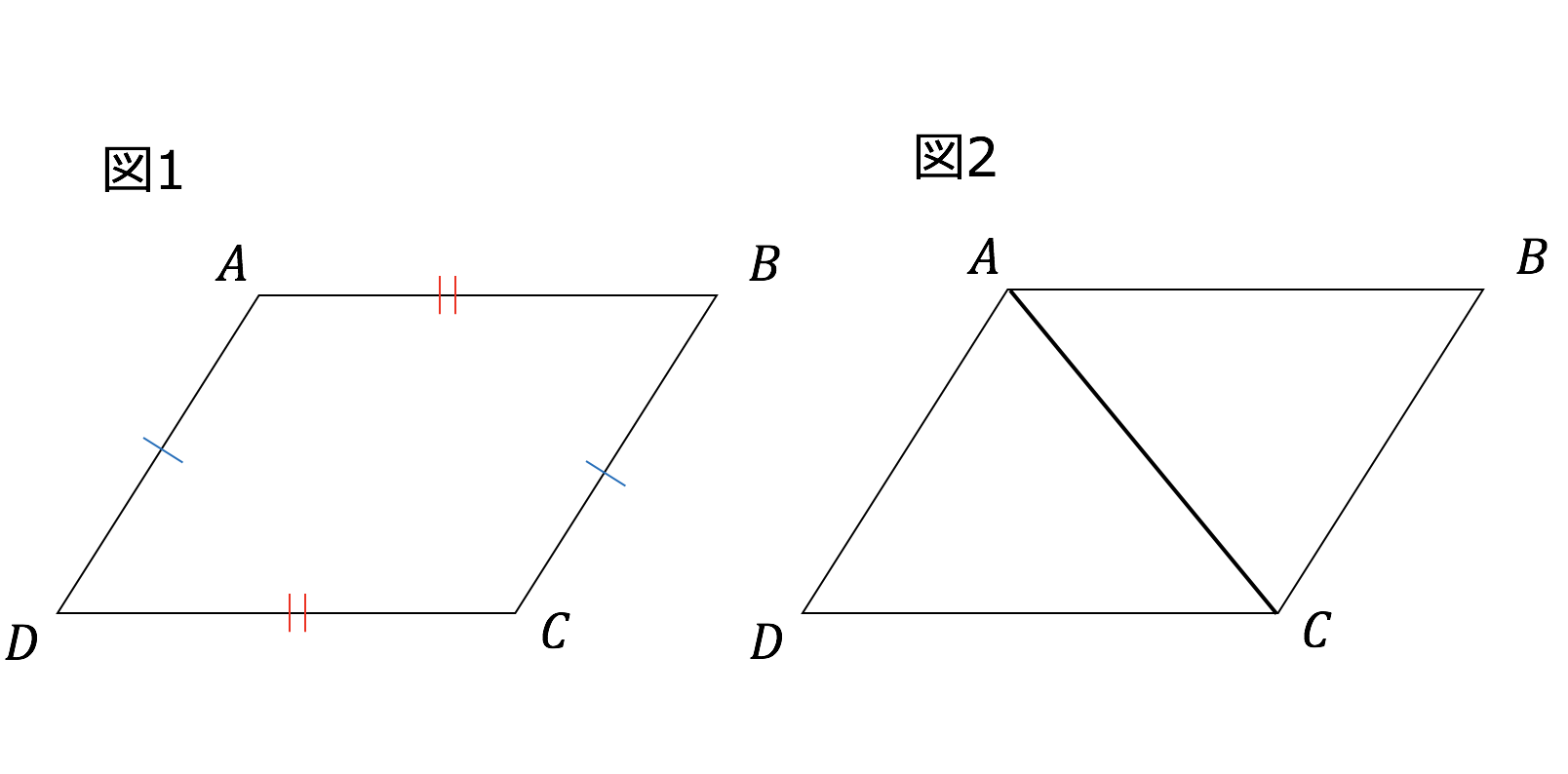 3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 | 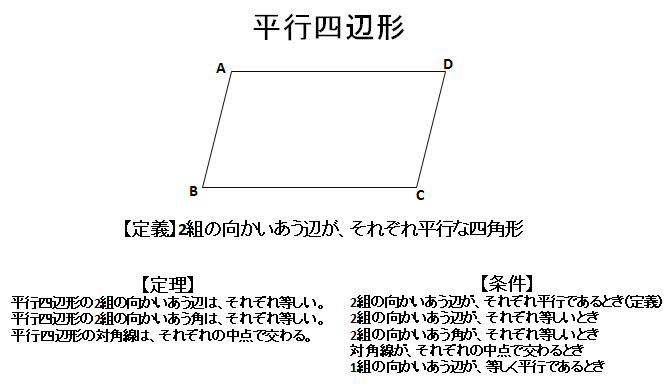 3 |  3 |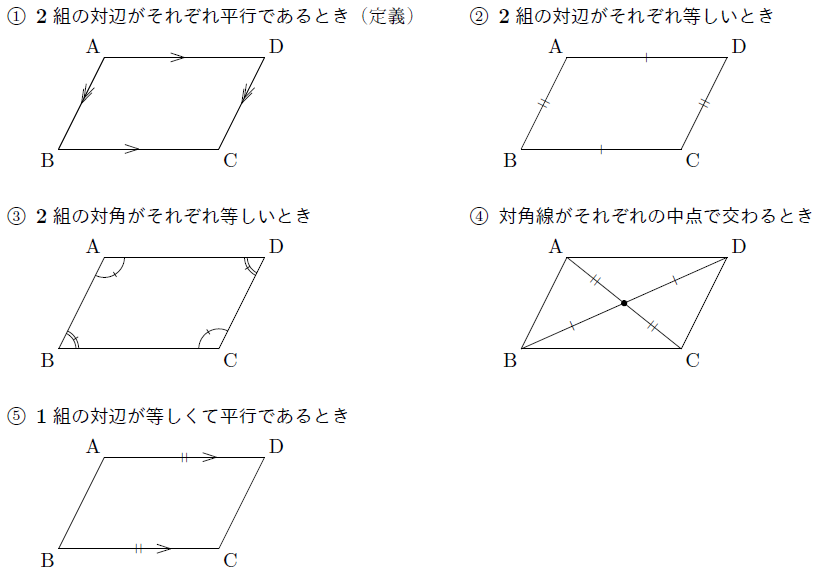
3 |  3 |  3 |
 3 |  3 |  3 |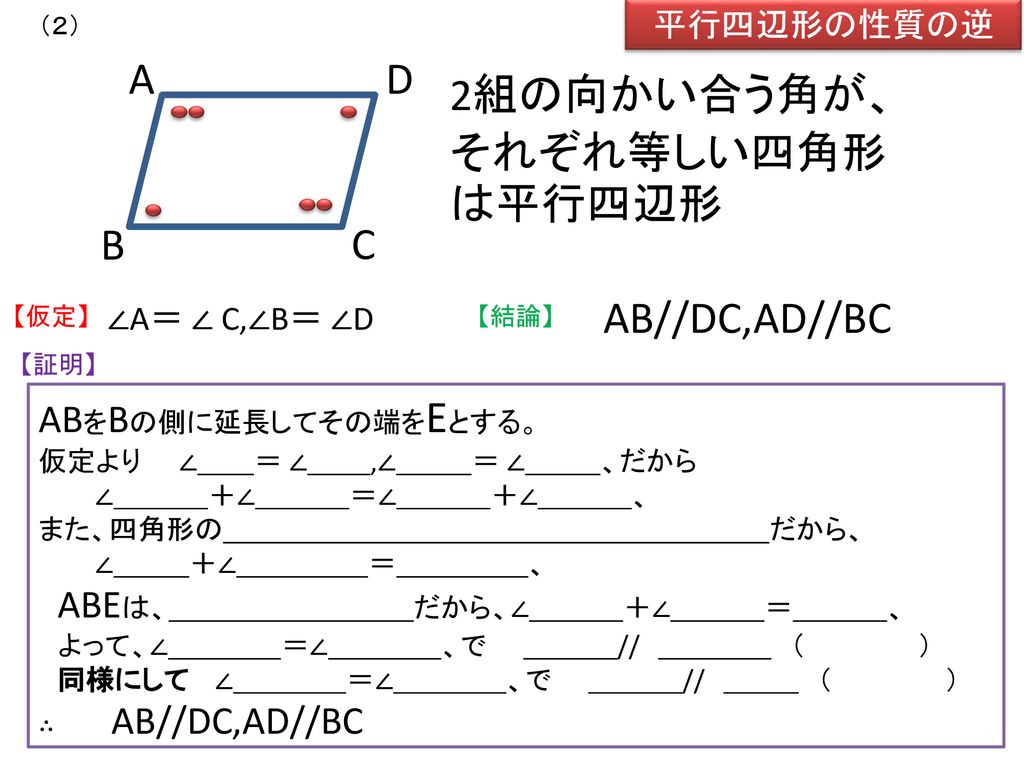
 3 |  3 |  3 |
 3 |  3 |  3 |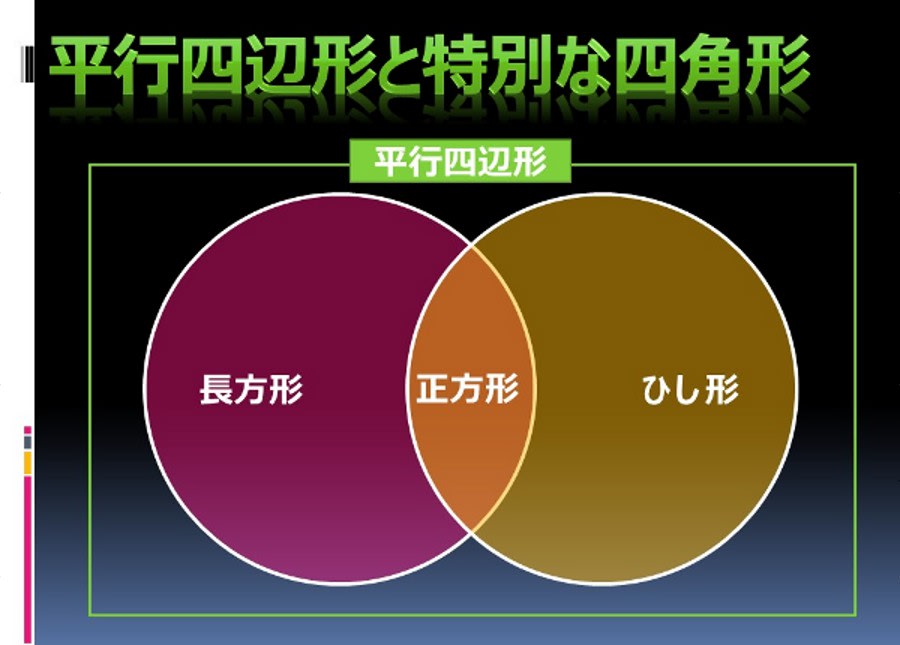
 3 | 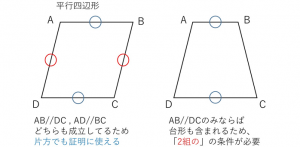 3 |  3 |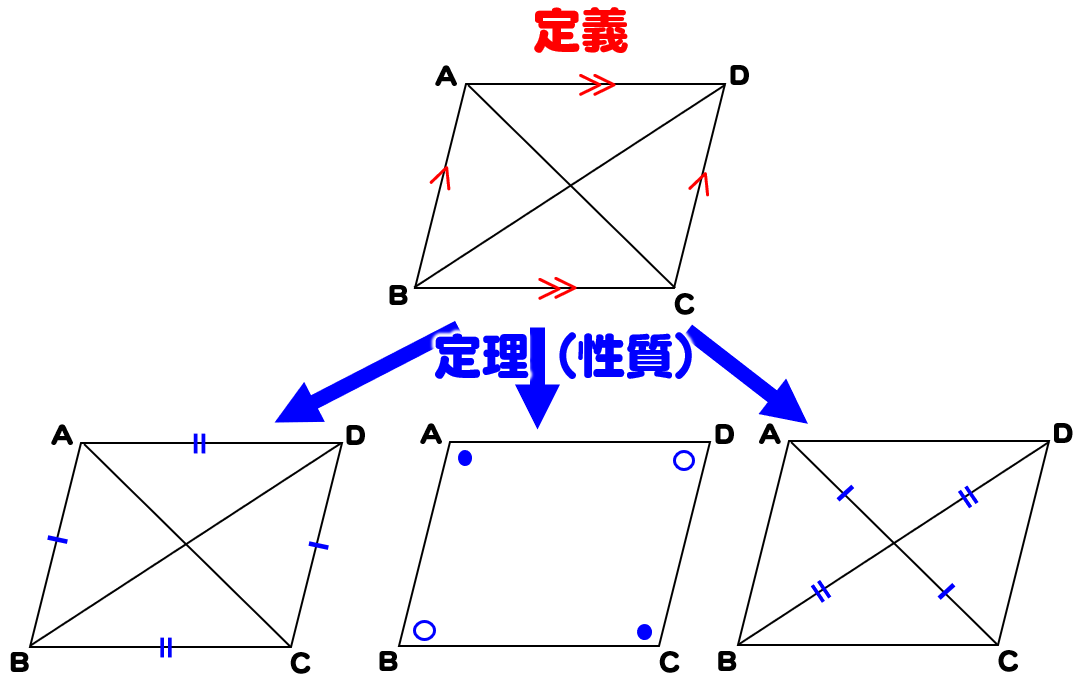
 3 |  3 |  3 |
 3 | 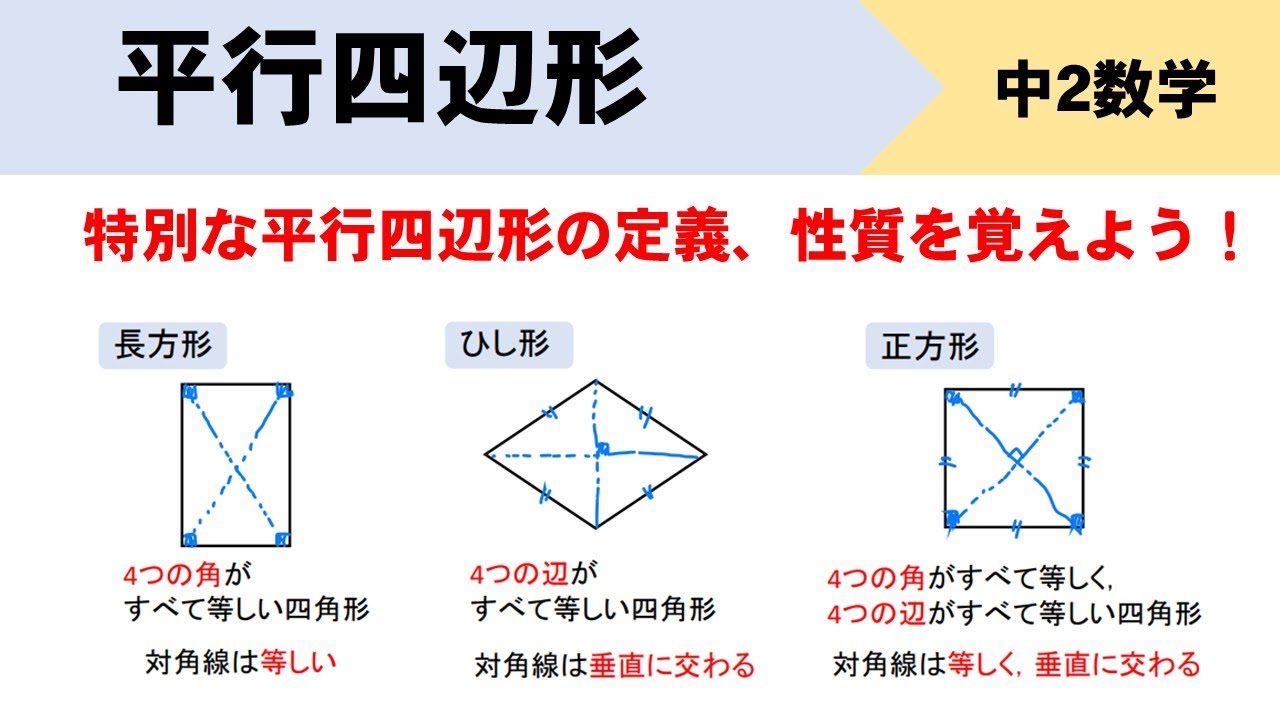 3 |  3 |
 3 | 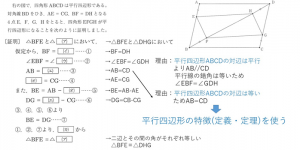 3 |  3 |
 3 |  3 |
平行四辺形 ・ ・ 長方形 ・ 定理（性質） ・ ・ ・ ・ ・ ・ 直角三角形の合同条件 ・ ・ ・ ・ 定理（性質） 二等辺三角形 ・ ・ 正三角形 ・ ・ ・ 三角形の合同条件 ・ ・ 条件・定義・定理（性質）確認プリント Title 図形の性質と合同条件・定義・定理 Created Date 2/4/16 PM まず平行四辺形の定義(意味)は「2組の対辺がそれぞれ平行である四角形」のことです。 平行四辺形に関する問題は中学2年生の数学で学習することが多いと思います。そして、「平行四辺形には、こんな定理(性質)があるよー」みたいなことを習います。その覚えておきたい定理は全部で下の4つです。 定理1：2組の対辺はそれぞれ等しい 定理2：対角線は
Incoming Term: 平行四辺形の定義 定理,
